Information
Authors: V. Nemkov, R. Goldstein, K. Kreter, and J. Jackowski
Location/Venue: HES 13 Padua, Italy
Topic: Modeling Cold Crucible Melting
Download Full Paper
Download Presentation
Abstract
Cold Crucible Furnaces (CCFs), widely used in multiple special applications of melting metals, oxides, glasses and other materials [1], are essentially 3D devices and their modeling is a complicated task. Multiple studies of CCFs have been made for their optimization, but their electrical efficiency is still low; for metals approximately 25-30% and even lower. Fluxtrol, Inc., made an extensive study of electromagnetic processes of CCFs using computer simulation and laboratory tests. This study showed that electrical efficiency of CCFs may be strongly improved by means of optimal design of the whole system with use of magnetic flux controllers. Theoretical results had been confirmed by laboratory tests on mockups and by industrial tests with real melting processes. The presentation contains a description of the computer modeling procedure and major findings. They form a basis for optimal design of electromagnetic systems of CCFs.
Introduction
Cold Crucible Furnaces are important for melting of metals and other materials in controlled conditions. It is typical for melting highly reactive metals, such as Zr, Ti and its alloys, etc. In a cold crucible, the amount of impurities introduced into the melt can be low. A significant part of the melt has no direct contact with the crucible due to electrodynamic forces confining the melt.The metal in contact with the CCF forms a solid layer – skull, that prevents the contact of liquid metal with copper and reduces thermal losses from the melt.
A draw back in the technology is low electrical and thermal efficiency. The crucible itself has high losses. To allow penetration of the magetic field through the crucible, thin axial slits are made in the walls. With the slits, the crucible wall is broken up into a set of fingers. Current is induced around each finger, resulting in a loss in effiency. Additionally, copper end caps on the crucible further reduce efficiency, since they act as Faraday rings. Sometimes they are in place for the purpose of containing the melt, and can be split to reduce losses; they are often used for shielding purposes.
CCFs have low thermal efficiency compared to other melting crucibles. A crucible made of a refractory material insulates the melt well, due to its low thermal conductivity, while a CCF hot metal is in direct contact with water-cooled copper. While improving thermal efficiency would be a challenge, there is a good opportunity to improve electrical effieincy of CCFs which we investigated.
Study Description
In this study, we investigate how the use of magnetic flux controllers can reduce power losses and improve the efficiency of CCFs. A mockup CCF, shown in figure 1 (left), was designed and manufactured for testing.
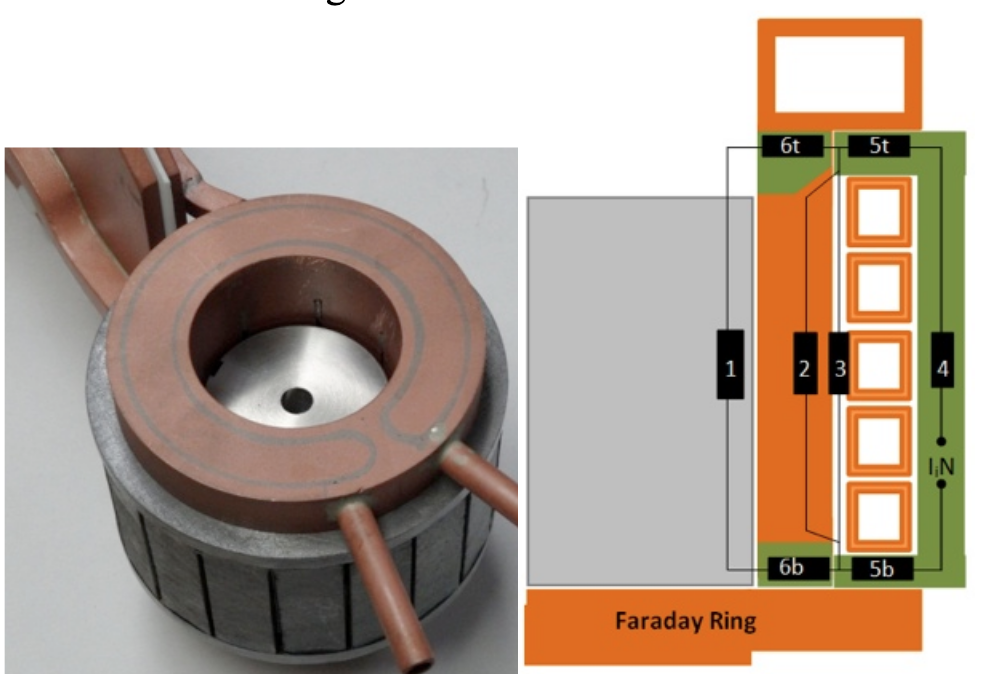
Figure 1: Picture of mockup CCF (left); magnetic circuit (right)
This mockup represents, rather well, real CCFs used for metal melting with bottom metal pouring. The crucible has 8 fingers and a cooling path at the tophead that does not extend into the fingers. Our tests were carried out at relatively low power levels, so additional cooling in the fingers was not necessary. The coil has five turns of square tubing and a Faraday ring below. Important dimensions of the CCF are listed in table 1.
Table 1. Dimensions of CCF used in the study (mm)
| Crucible ID | Crucible OD | Finger Slit Width | Coil ID | Coil Length | Coil Tubing | Load OD |
|---|---|---|---|---|---|---|
| 60.20 | 82.55 | 2.03 | 88.85 | 53.92 | 9.53 x 9.53 | 57.00 |
Flux concentrator was machined and applied in three forms: shunts, inserts and a flat ring. The material used was Fluxtrol 100. Two coils were manufactured, with one having shunts around it. The shunts consist of strips placed along the back of the turns and circular top and bottom poles. Shunts of Fluxtrol flux concentrator are already being used in practice.
Inserts and the concentrator ring are new applications that are being investigated in this study for the first time. It was hypothesized that they would improve the penetration of magnetic field through the CC fingers, and reduce losses in the CC fingers and Faraday ring. The inserts were placed between the slits of the crucible. They extended from the ID to the OD and were approximately 1 cm tall. Inserts could be placed on both the top and bottom of the slits. The flat ring of concentrator was used as an alternative to the bottom insert. The piece had the same ID and OD as the crucible and was only 1.5 mm thick. It was placed in the space between the Faraday ring and crucible.
The magnetic circuit of the CCF consists of the six components labeled in figure 1: 1 corresponds to the load, 2 to the zone of the axial field penetration through the CC, 3 to the gap between the coil and crucible, 4 to the return path, 5 to the gap between the coil and Faraday ring, and 6 to the zone of radial field flow along the CCF fingers.
Experiments on the physical cold crucible unit were made to verify simulation results and to test the manufacturing technique. The cold crucible was tested using varying arrangements of flux concentrator. Tests were conducted at 10 kHz, and current and voltage were measured to find impedance of the CCF. To determine the load power, calorimetry was used. Constant power was held for a fixed amount of time and the load was moved to a calorimeter. The temperature change of the water was recorded and used to calculate power into the load. Finally, a magnetic field probe was used to map the field strength profile between the load and crucible and see the difference between flux controller arrangements.
Using 3D finite element simulation we are able to analyze in detail the EM fields and calculate parameters of the CCF. A 3D wedge with the same dimensions of the physical mockup CCF was simulated under the same current level of 200 A. The coil impedance, load resistance, and field distribution were compared to the experimental resuts to verify the simulation. The simulation was then used to get results that the experimental setup could not, including losses in each individual CCF component.
Infinitely Long Cold Crucible Furnace
As a basis for analysis, we developed a set of analytical equations to describe an infinitely long cold crucible. The results from this analysis give the maximum possible efficiency that can be achieved for a selected system cross section. We could then benchmark the results from 3D simulation against the infinitely long case, and see how close we were with magnetic flux control to the ideal case. The CCF is “infinite” in that the radial magnetic field on the ends is not taken in consideration. We calculate the load, fingers, coil winding, and overall impedance of the mock-up CCF. The equations can also be applied to any long CCF to calculate their parameters. All impedances are “transferred” to the N-turn winding.
2D Simulation of CCF
A method was also developed and used in practice at Fluxtrol, Inc., for sevaral years to make 2D CCF simulation [2]. In other studies different methods for 2D CCF simulation have been developed [3,4]. The challenge when trying to model a CCF in 2D is modeling the crucible finger region, since otherwise it is an axisymmetrical system. The slits between the fingers make CCFs a 3D problem. To account for the fingers, the space of the CCF wall was filled with a non-conductive material with a certain equivalent permeability. The equivalent permeability must give the same reluctance for the fictitious material as for a real CCF. Equivalent permeability must be anistropic due to the fingers geometry. Equation 5 is used to calculate permeability in the radial and axial direction. The parameters is mean circumferencial finger width, t is the crucible wall width, and b is the sum of s and h. μr,slits is permeability of inserts for areas where they are installed and is 1 for areas without them.
There is a significant difference between equivalent permeability in the radial and axial directions (μeq,radial,air= 0.077, μeq,axial,air= 0.142), which influences the magnetic field orientation along the finger. The latest version of Flux 2D is capable of defining anistropic properties, improving the accuracy of 2D CCF modeling. Figure 2 shows the magnetic field lines for a CCF with shunt, inserts, and ring (right) and a CCF with no flux concentrator (left). They correspond well to magnetic scheme of Figure 1.

Figure 2: Magnetic field lines from 2D simultation.
2D simulation provides the possibility to visualize the magnetic field distribution and calculate rather accurately the coil inductance, coil losses, and load power. While the magnetic field can be properly defined in 2D models, losses in the fingers cannot be calculated directly. Losses may be calculated additionally based on the magnetic field distribution; however, an error in losses is still significant because the 2D model can’t describe axial current flow in the end zones of the fingers. 2D CCF modeling is a good engineering tool to use for preliminary calculations and matching, since developing a 3D model is more challenging, time consuming, and expensive.
CCF Simulation Using FLUX 3D
There is much research in magnetohydrodynamics (MHD) of the melt in a CCF [4,5]. For MHD research, results from electromagnetic simulation are required for the basis of calculations. In this study, a finite element electromagnetic model of the CCF was made using Flux 3D. To simplify the model, only a 1/8 wedge of the system was modelled. A periodicity boundary condition was applied to the sides of the wedge. For those boundary conditions, the mesh nodes on each side of the wedge must be the same. Output results for active and reactive powers simply had to be multiplied by the number of wedges to make up the whole CCF. Superconductive boundary conditions were applied to the outer surfaces of the model. The resistivity of low temperature copper was applied to the coil and crucible components including the Faraday ring and fingers. Stainless steel was used as the load. Fluxtrol 100 was selected as the magnetic material for the shunts, inserts, and ring, and the corresponding BH curve was applied in the model. Figure 3 shows the wedge used in 3D simulation of the CCF. It is shown meshed with and without flux concentrator; current density is shown in the coil, fingers, and Faraday ring without flux concentrator. The load and air regions are not shown.
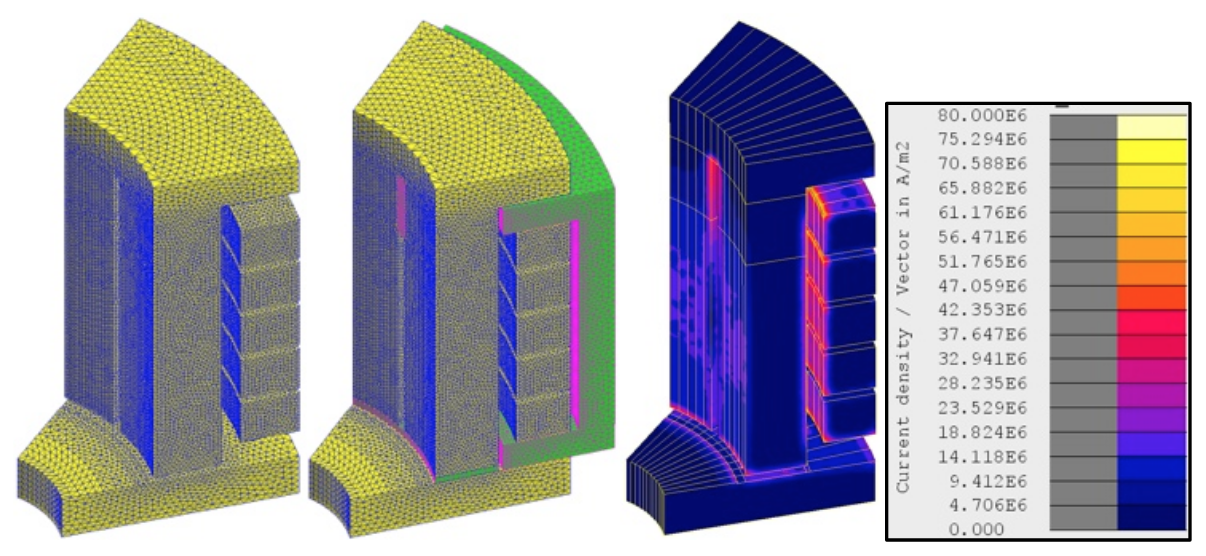
Figure 3: CCF wedge in 3D simulation; meshed wedge without (left) and with (center) flux concentrator; current density in CCF without concentrator (right) with no load shown
Simulations were made for five different cases for comparison. The first simulation was for a bare coil with no concentrator as the worst case to compare the others to. The other four cases had different combinations of flux concentrator applied: top inserts only, top inserts and Fluxtrol ring, shunt with top inserts, and full concentrator with top inserts, shunt and Fluxtrol ring. A constant current of 200 A was applied to the coil in all cases. Table 2 contains the results from simulation, experiments, and the infinitely long case for comparison.
Table 2. Results for impedance, load resistance, and efficiency from simulation, experiments, and the infinitely long case
| Shunt | No | No | No | Yes | Yes | – | |||||
| Top Insert | No | Yes | Yes | Yes | Yes | – | |||||
| Fluxtrol Ring | No | No | Yes | No | Yes | – | |||||
| Experimental (E) Simulated (S); Infinite (I) | E | S | E | S | E | S | E | S | E | S | I |
| Impedance (Ohm) | 42.9 | 41.6 | 48.3 | 45.9 | 49.5 | 47.6 | 68.6 | 72.0 | 73.0 | 76.1 | 77.2 |
| Load Resistance (Ohm) | 1.61 | 1.70 | 2.84 | 2.66 | 3.55 | 3.50 | 5.10 | 6.48 | 7.16 | 8.92 | 12.9 |
| Efficiency (%) | – | 25.4 | – | 35.3 | – | 42.5 | – | 43.9 | – | 52.7 | 53.2 |
| Power Factor | – | 0.16 | – | 0.16 | – | 0.17 | – | 0.21 | – | 0.22 | 0.31 |
The results show a great improvement with the addition of the whole magnetic circuit. The resistance of the load transferred to the coil increases more than 5 times, and electrical efficiency doubles. Each component of the magnetic circuit is important, since there is a significant improvement in the results for each part added. The results for impedance and load resistance from simulation approach the values from the infinitely long case. This indicates that with the shunt, top insert, and Fluxtrol ring the CCFs electrical efficiency gets close to the maximum possible value.
The results in table 2 show good agreement between the Flux 3D and experimental results. This agreement supports the validity of the 3D models. We also made a comparison of the axial magnetic field distribution. The distribution for the 5 cases from both our experimental and simulated results is shown in figure 4. In all cases the current is 200 A, and the field is measured along the outer surface of the load in the middle of the CC finger face.
The distributions further demonstrate the improvements made by applying flux control to the CCF. The flux density more than doubles from the bare CCF case to the case with flux concentrator fully applied. The effect of the Fluxtrol Ring is demonstrated between curves 4 and 5. The addition of the ring raises the flux density at the bottom of the distribution, while the top of the distribution remains almost the same. This shows how flux control can be used to change the distribution of the heat in the load. By adding a Fluxtrol ring, heating of the bottom of the melt can be increased, while holding the heating at the top constant. The top insert has the similar affect, so it can be used to control the distribution of heating at the top of the melt.
Major Findings
Our results showed major improvements with the use of flux concentrators to optimize CCFs. The next task was to describe the source of the improvements, and explain how adding each type of concentrator influences the CCF parameters.
Shunts of Fluxtrol concentrator on induction coils is a commonly seen application of flux control. Placing a material with high magnetic permeability around the coil, we increase the magnetic field strength on the part surface for the same coil current or the coil current may be reduced for the same heating effect. Losses are proportional to current squared, so this explains some of the improvement in efficiency seen in our simulations. Supplying circuitry is not included in our simulation, and we’d expect that the reduction in current would also reduce the losses in the coil leads, cables, capacitors, etc., further improving the system efficiency. Figure 5 shows current density in the coil from simulation for cases without shunts, with shunts, and with shunts and inserts. The power in the work piece is held constant at 7.4 kW for this analysis. With only the addition of shunts, the coil current is reduced from 2205 A down to 1653 A. When inserts are also used, coil current is further reduced to 933 A.
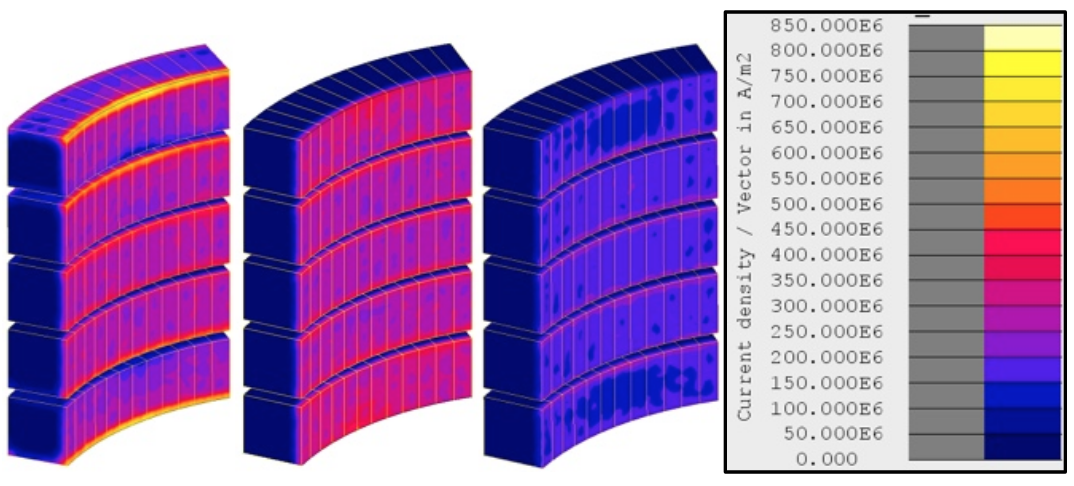
Figure 5: Current density in the coil without shunts (left), with shunts (center), and with shunts and inserts (right); corresponding values of the coil currents are 2205, 1653 and 933 A
The addition of the Fluxtrol ring reduces losses in the Faraday ring due to shielding effect. Figure 6 shows current density in the Faraday ring, with and without inserts.
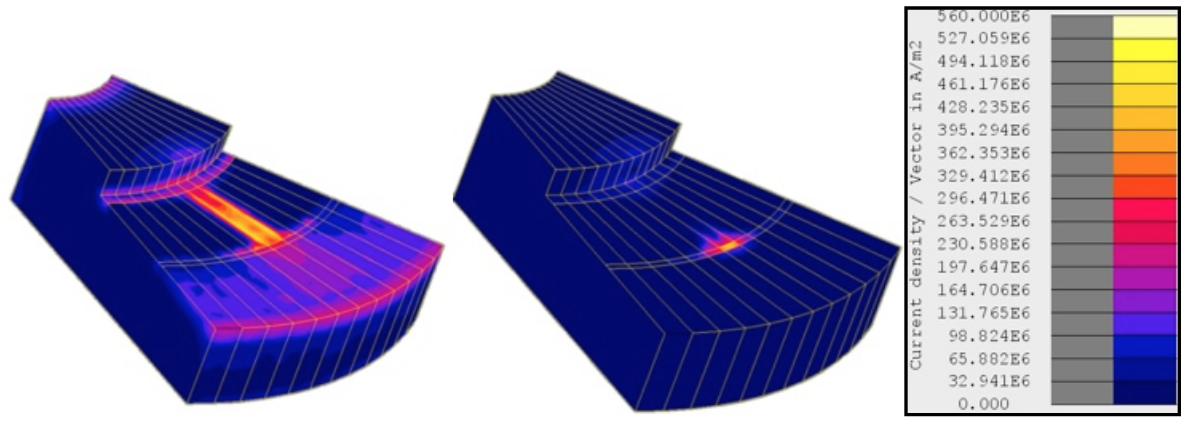
Figure 6: Current density in the Faraday Ring without inserts (left) and with inserts (right)
The crucible fingers are a major source of losses in CCFs. The crucible slits are in place to allow penetration of the magnetic field through the crucible. With no flux control, there are essentially two main current components in the fingers. First there is current induced by the axial magnetic field in the CCF; it flows around the fingers. The other current portion induced by the radial magnetic field in the end zones of CC. This current flows along the fingers closing at their ends. When an insert and Fluxtrol ring are used, the axial current is strongly reduced. The insert reduces the magnetic field strength in the slit, while keeping the total magnetic flux almost the same. Figure 7 shows the current density in the finger with and without magnetic inserts. Image 7b is 7a rotated 90 degrees, and 7d is 7c rotated 90 degrees.

Figure 7: Current density in the finger without inserts (7a & 7b) and with inserts (7c & 7d)
If you compare the surface of the finger facing the melt (left side of 7a and 7c) for the two cases the current density is approximately the same. This is because the magnetic field on the load face must be the same, since power in the load is held constant. The other faces of the finger (7b and 7d) show a dramatic difference with and without flux control. The reduction of the current along the length of the finger is the reason for this difference. Using flux control, the axial current in the finger is greatly reduced, reducing the losses in them. Table 3 details the power distribution in the CCF with different combinations of flux control. The power in the load is held constant between the cases.
Table 3. Results for power distribution in CCFs with varying flux control
| Shunt | No | Yes | No | Yes | |
| Inserts (Top and Bottom) | No | No | Yes | Yes | |
| Power (kW) | |||||
| Load | 7.4 | 7.4 | 7.4 | 7.4 | |
| Coil | 10.6 | 7.7 | 5.1 | 2.5 | |
| Faraday Ring | 1.0 | 0.4 | 0.7 | 0.7 | |
| Cooling Head | 0.6 | 0.3 | 0.5 | 0.1 | |
| Fingers | 11.0 | 12.0 | 5.2 | 4.9 | |
| Total | 30.6 | 27.8 | 18.8 | 14.7 | |
Flux control was tested in a real CCF system for melting by Retech Systems [6]. Shunts around the coil and inserts in the slits were both applied to the CCF. A significant improvement in efficiency was seen in the tests. To protect the inserts from the melt, grout was used in the internal parts of the slits with much success.
Conclusions
Results from 3D simulation and experiments showed that with magnetic flux control, the electrical efficiency of CCFs can be greatly improved. The mockup CCF used in this study has an efficiency of only 25.4% without flux control, and efficiency is doubled when it is applied. A method was developed to calculate the efficiency of an infinitely long CCF that would indicate the maximum possible improvement in electrical efficiency. Using shunts, inserts, and the ring of magnetic concentrator the efficiency was improved to near that maximum. Magnetic shunts reduce the coil current, and reduce losses in the supplying circuitry, size of the generator and capacitor battery. Slit inserts strongly increase efficiency and reduce coil current demand. While both shunts and inserts bring improvements alone, their combination has a much larger effect. For the same power in the load, magnetic flux control in the selected CCF reduced the generator power 2 times and the size of the capacitor battery almost 3 times. For future CCF designs, the addition of magnetic flux control to the system should be an essential means for the system efficacy improvement.
References
[1] Muhlbauer, A., (2008). History of Induction Heating & Melting. Vulkan Verlag. [2] Heidloff, A., et al. (2011). Advancements in Ti Alloy Powder Production by Close-Coupled Gas Atomization. Advances in Powder Mettalurgy& Particulate Materials. [3] Westphal, E., Muiznieks, A., Muhlbauer, A. (1996). Electromagnetic Field Distribution in an Induction Furnace with Cold Crucible. IEEE Trans. on Magnetics, 32, 1601-1604. [4] Umbrasko, A., Baake, E., Nacke, B., Jakovics, A., (2007). Numerical Studies of the Melting Process in the Induction Furnace with Cold Crucible. HES-07. 277-292. [5] Bojarevics, V., Pericleous, K. (2001). Modelling Induction Melting Energy Savings. International Scientific Colloquium, Modelling for Savings Resources, 11-16. [6] Haun, R., Charles, M., Lampson, R., et. al. (2013). Recent Design and Operat. Devel. of Cold Crucible Induction Furnaces for Reactive Metals Processing. HES-13.If you have more questions, require service or just need general information, we are here to help.
Our knowledgeable Customer Service team is available during business hours to answer your questions in regard to Fluxtrol product, pricing, ordering and other information. If you have technical questions about induction heating, material properties, our engineering and educational services, please contact our experts by phone, e-mail or mail.
Fluxtrol Inc.
1388 Atlantic Boulevard,
Auburn Hills, MI 48326
Telephone: +1-800-224-5522
Outside USA: 1-248-393-2000
FAX: +1-248-393-0277
